\(\longrightarrow\) Puissance d'une force (indique le rythme auquel le travail est éffectué)
On sait que \(\delta W=\vec F.\vec{dl}=\vec {F}.\vec v.dt\)
$$P={{\frac{\delta W}{dt}=\vec F.\vec v}}$$
P: en \(J.s^{-1}\)
Théorème de la puissance cinétique
Le théorème de l'énergie cinétique permet d'écrire: \(dE_c={{\sum_i \delta W_i=\sum_i \vec F_i.\vec v.dt}}\)
\(\iff\) \(dE_c={{\sum_iP_i.dt}}\)
\(\implies\) Formule du TPC:
$$\frac {dE_c}{dt}=P$$
\(\longrightarrow\) Exemple: pendule simple
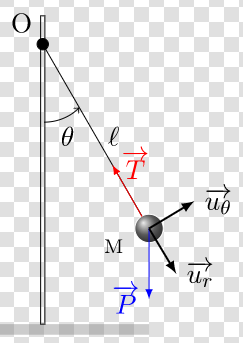
La bille de masse m est un point matériel dans un référentiel supposé galiléen.
On utilisera la base intrinsèque \((\vec e_t, \vec e_n)\)
On suppose qu'il n'y a pas de frottement.
1) \(\overrightarrow {OM}= -l.\vec e_n\)
\(\vec v=\frac{d\overrightarrow {OM} }{dt}= l.\dot\theta.\vec e_t\)
2) \(E_c=\frac 12.m.v^2=\frac 12.m.l^2\dot\theta^2\)
\(\frac{dE_c}{dt}=\frac 12 m.l^22\dot\theta.\ddot\theta=ml^2\dot\theta\ddot\theta\)
3) \(P=\sum_iP_i=P_{\vec P}+P_{\vec T}\)
\(P_{\vec T}=\vec T.\vec v\) et \(\vec T \perp \vec v\) \(\implies\) \(P_\vec T=0\)
\(P_{\vec P}=m\vec g.\vec v=\begin {pmatrix}-mg\sin\theta\\ -mg\cos\theta\end{pmatrix}\begin {pmatrix}l\dot\theta\\ 0\end{pmatrix}\)
Par le théorème de la puissance cinétique:
\(\frac {dE_c}{dt}=\sum_iP_i=P_{\vec P}\)
\(ml^2\dot\theta.\ddot\theta=-mgl\dot\theta\sin \theta\)
\(l\ddot\theta=-g\sin \theta\)
\(\ddot \theta=-\frac gl\sin \theta\)
Aux petits angles: \(\sin \theta\simeq\theta\)
\(\implies\)Donc: $$\ddot \theta=-\frac{g}{l}\theta$$
$$\ddot\theta=-w_0^2\theta$$
Avec \(w_0\): la pulsation propre du pendule